前言
大家好,我是来自「华为」的「小熊」。端午假期马上就要结束了,小熊给大家带来一道笔试和面试中与「动态规划」相关的常考的简单题,这道题被字节、微软、亚马逊和苹果等各大互联网大厂作为笔试题。
这道题就是 Leetcode 的第 53 题-最大子序和,了解「动态规划」的童鞋,在看到最大两个字的时候,很容易就会想到用「动态规划」去解答,因为涉及到「最优解」的问题,一般都可以通过动归去做。本题小熊提供「动态规划」的思路供大家参考,希望对大家有所帮助。
题目
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素), 返回其最大和。 示例 1: 输入:nums = [-2,1,-3,4,-1,2,1,-5,4] 输出:6 解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。 示例 2: 输入:nums = [1] 输出:1 提示: 1 <= nums.length <= 3 * 10^4 -10^5 <= nums[i] <= 10^5
解题思路
本题是一道典型的「动态规划」的题,因此采用动态规划的策略去解答。
「定义状态」
dp[i]:以nums[i]结尾(包含nums[i])的连续子数组的最大和。
「状态转移方程」
dp[i]=max(dp[i-1]+nums[i],nums[i]),其中i>=1,当dp[i-1]<0 时,抛弃当前的和最大的连续子数组,从nums[i]开始重新寻找和最大的连续子数组,否则将nums[i]加入到当前的和最大的连续子数组。
「边界条件」
dp[0] = nums[0]。
「举栗」
以数组nums[i]=[-2,1,-3,4,-1,2,1,-5,4]为例子,如下图示。
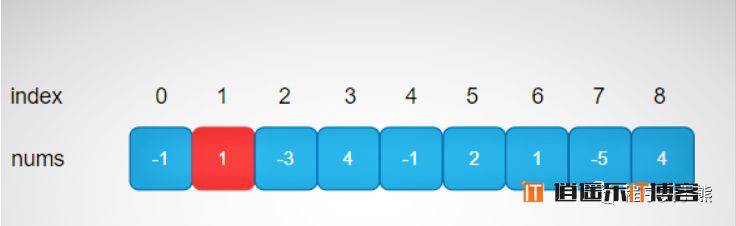
从上图可以看出:dp[0] = nums[0] = -1 < 0,由于当前的连续子数组的最大和小于零,因此应该丢弃 num[0],从 nums[1] = 1 开始重新寻找和最大的连续子数组。
寻找和最大的连续子数组的完整动图,如下所示:
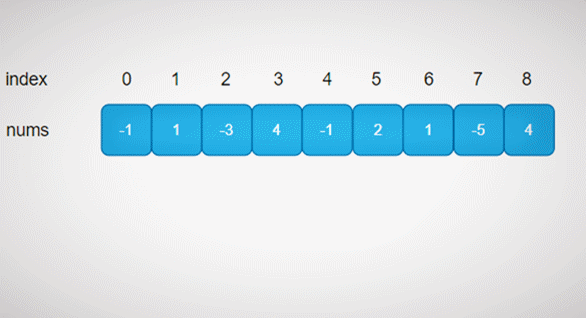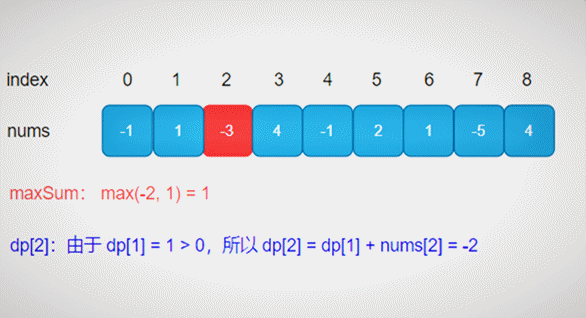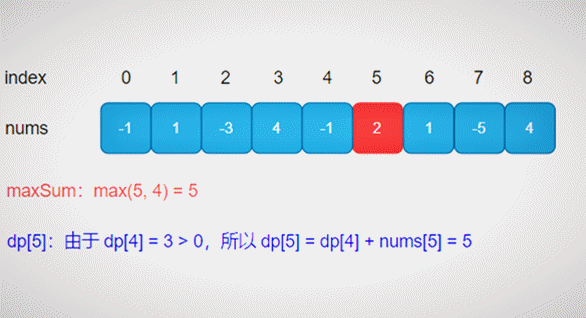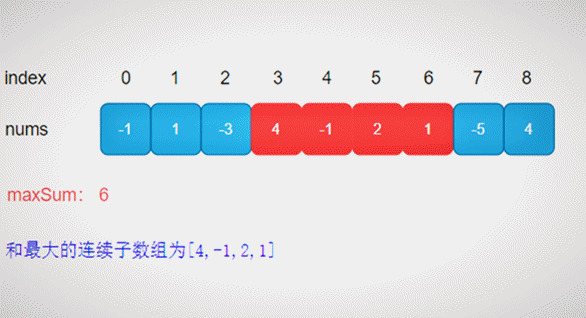
由状态转移方程可知,dp[i]只与dp[i-1]和nums[i]相关,因此没必要再去定义dp,直接复用nums即可。
Show me the Code
「C++」
int maxSubArray(vector<int>& nums) {
int maxSum = nums[0];
for (int i = 1; i < nums.size(); ++i) {
nums[i] = max(nums[i - 1], 0) + nums[i];
maxSum = max(maxSum, nums[i]);
}
return maxSum;
}
「Java」
int maxSubArray(int[] nums) {
int maxSum = nums[0];
for (int i = 1; i < nums.length; ++i) {
nums[i] = Math.max(nums[i - 1], 0) + nums[i];
maxSum = Math.max(maxSum, nums[i]);
}
return maxSum;
}
「Python3」
def maxSubArray(self, nums: List[int]) -> int:
for i in range(1, len(nums)):
nums[i] = max(nums[i - 1], 0) + nums[i]
return max(nums)
「Golang」
func maxSubArray(nums []int) int {
maxSum := nums[0];
for i := 1; i < len(nums); i++ {
if nums[i - 1] > 0 {
nums[i] += nums[i - 1]
}
if nums[i] > maxSum {
maxSum = nums[i]
}
}
return maxSum;
}
「C」
int maxSubArray(int* nums, int numsSize){
int maxSum = nums[0];
for (int i = 1; i < numsSize; ++i) {
nums[i] = fmax(nums[i - 1] + nums[i], nums[i]);
maxSum = fmax(maxSum, nums[i]);
}
return maxSum;
}
「复杂度分析」
时间复杂度:「O(n)」,其中参数 n 是数组中元素的个数,需要遍历一遍数组。
空间复杂度:「O(1)」,未开辟额外的存储空间。


最新评论